BIOL 4120 Principles of Ecology Phil Ganter 330 Harned Hall 963-5782

Modeling Density-Dependent Population Growth

Email me

Back to:

Lecture 11 Population Regulation

This is the first modification of the equation for exponential growth:

dN/dt = rN

A modification of this equation is necessary because exponential growth can not predict population growth for long periods of time. No matter how slowly a population grows, exponential growth will eventually predict an infinitely large population, an impossible situation. So we need to modify this growth rate to accommodate the fact that populations can't grow forever.

• To do this we will add a term that will reduce dN/dt as the population increases. There are many ways to do this. One way was originated by P. F. Verhulst in 1839 &endash; perhaps one of the oldest publications still influential in ecology &endash; and fully developed by A. J. Lotka in 1925. The approach involves thinking about what might happen in a more realistic situation.
• Let's consider the first assumption of exponential growth: constant r (= constant b and d, where b and d are the instantaneous birth and death rates, respectively). This is not very realistic, as both birth and death rates will vary. Lets assume that they depend on the population size, so that one can predict b or d using the population size.

There are many ways to model the relationship between population size and b or d. The simplest is a linear relationship, such that a linear equation can be used to predict b (or d) given N:

d = d₀ + zN

• Here, we see that the death rate begins a some level (d₀) near 0 and increases as N increases (v is the slope, which converts N into d,). This makes sense, as more individuals living on the same resources are likely to have a higher mortality.
• To see what this relationship looks like, scroll down to the figure below and you will see the line and a visual explanation of z.

Take a moment to consider units, which are the key to understanding mathematical models. If d is an instantaneous rate of population change its units are individuals/(individuals*time). The numerator is obvious as we are changing the number of individual when a population grows or shrinks. The denominator means that the rate depends on time (as rates tend to do) and the individual. So r, b and d are all per capita rates. As z converts between N and d, its units must be 1/(individuals*time), so that when you multiply it by N individuals, you get the right units for d (be aware that one cannot add two numbers if they do not have the same units, a fact that is often assumed by writers of equations but forgotten by those reading equations).

We have to slightly change the equation for b, as the birth rate should decrease with mortality (given more individuals and the same resource base).

b = b₀ - vN

• Here, b₀ is the maximal birth rate and b will equal this when N is close to 0 and resources per individual are greatest.
• As above, look at the diagram below to see an explanation of v.

Now rewrite the equation for exponential growth keeping in mind that r = b - d:

dN/dt = rN = (b - d)N

• We can substitute for b and d in this equation:

dN/dt = [(b₀ - vN) - (d₀ + zN)]N

or

dN/dt = [(b₀ - d₀) - (v + z)N]N

• This equation describes population growth rates when birth and death rates depend on N in a linear fashion. Now we have to do something that is mathematically correct, but the reason for doing it will not be clear until a few steps lower. In essence, we want to derive a more useful form of the last equation above.
• We will multiply the right side of the equation by: (b₀ - d₀)/(b₀ - d₀)
• Since this is equal to 1, we are not changing the value of the right side.
• When we do this we get

dN/dt = [(b₀ - d₀)/(b₀ - d₀)][(b₀ - d₀) - (v + z)N]N

• rearranging this gives us:

dN/dt = (b₀ - d₀)[(b₀ - d₀)/(b₀ - d₀) - (v + z)N/(b₀ - d₀)]N

dN/dt = (b₀ - d₀)[1 - [(v + z)/(b₀ - d₀)]N]N

• Since b₀ and d₀ are the birth and death rates with no density effects, the difference between them is, by definition, r, so we can substitute r into the equation:

dN/dt = rN{1 - [(v + z)/(b₀ - d₀)]N}

We are almost there now. I hope you can see that it was useful to perform the not-so-obvious step as it gave us back an equation that is similar to one with which we are already familiar. Notice, however, that we have added a term to the original equation for exponential growth. It is this term that is the modification we are seeking: the term that alters population growth rates as the density of the population changes. This effect is called density-dependence in the sense that b and d are linearly dependent on the density of the population. Lets consider that term (I will call it the DD term) more closely as there are too many variables in it for convenience:

[(v + z)/(b₀ - d₀)]N

• We will now do a second not-so-obvious thing. We will define a new variable that is a combination of variables we already have. This can conveniently reduce the number of variables in the equation if done just right. We will define K as K = (b₀ - d₀)/(v + z)
• This is just the inverse of the fraction in the density-dependence term above. You might ask why we chose the inverse. Dimensions are the key again. We want a new term that is in the dimensions of individuals. This dimensionality is useful for two reasons. It makes K biologically meaningful, as it represents the number of organisms in the population when birth and death rates are equal. This is the carrying capacity of the environment (more on this below).
• Now we can rewrite the density-dependent population growth rate equation with K in it.

dN/dt = rN{1 - [1/K]N}

or

• which is equivalent to:

.

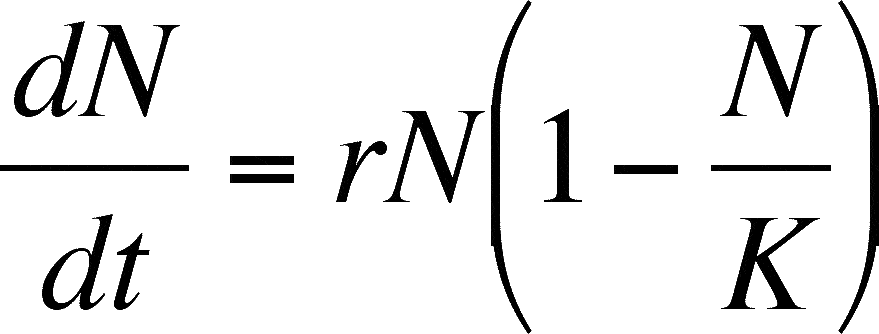
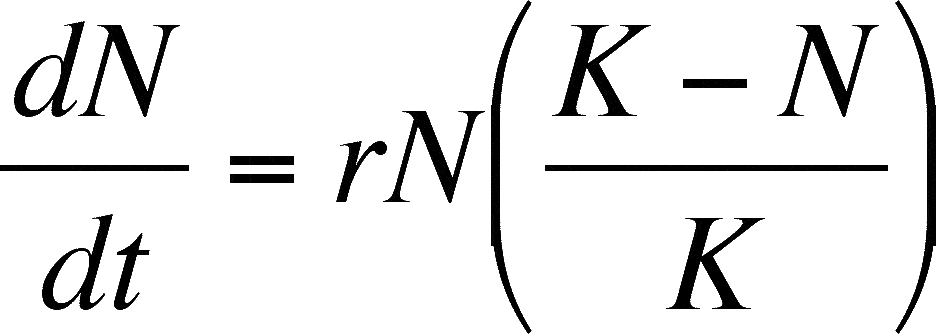• This is the form I will use in class.

This form of the equation is called the Logistic Equation. When N is small, the DD term is near 1 as the N/K term is small, and the population grows at near maximal rate. Notice what happens as N increases. As N approaches K, the N/K term comes near to 1 and when subtracted from 1 the DD term gets smaller and smaller, indicating that the population is growing at only a fraction of its potential. Eventually K and N are equal and the DD term becomes 1 &endash; 1 or zero. Growth stops (the growth rate is 0) when N = K (look above at the definition of K). The population is stationary (neither growing nor declining) and we call this population size the carrying capacity. This term implies that this is the maximal number of individuals that can be sustained in that environment. K is in units of individuals but is related to the amount of resource present and the amount of resource needed per individual.

• What happens if N exceeds K (if the actual population size exceeds the carrying capacity)? The DD term turns negative, as the N/K fraction is greater than 1. dN/dt, the population growth rate, then becomes negative and the population shrinks back to a population size at which the growth rate becomes 0 once again.
• Thus, the population grows when it is under K and shrinks when it exceeds K. K represents a stable equilibrium point. It is an equilibrium point because the population does not change when it attains that size. It is stable because the population will return to K if it becomes larger or smaller than K.

A word about the assumption of linearity. It is the simplest way to model the relationship between b, d, and N but it may not be very realistic. A curve of some sort is more likely to be realistic, as the effect of adding individuals may not be felt until some critical threshold in resource per individual has been crossed. Indeed, there may be an increase in birth rates (or a decrease in death rates) when individuals are added at low density (this is called the Allee effect after an ecologist interested in the benefits of living in groups). Below is a figure that shows the relationship between b, d, and K. Many other models have been used in which b declines with N and d increases, but the relationsip is a curve instead of the lines below.

In the diagram above, b₀ and d₀ are the Y-intercepts of the b and d lines respectively and v and z are the slopes of the lines. It it possible to calculate r, but only as b₀ - d₀ (the intercept values), the birth and death rates unaffected by density, as r is defined without any density effects. If you subtract the values at some density other than 0, you get the population growth rate at that density. K is easy to find because it is the point at which population growth is zero, and that will happen when b₀ = d₀, which is the intersection of the two lines.

The assumptions of the logistic include all of the assumptions found in the model it is based on: the exponential growth model with the exception that there be a constant b and d. To review those assumptions go to Modeling Exponential Growth. We modified the equation by violating the assumption of constant birth and death rates. In doing so, however, we have added other assumptions"

1. The relationship between density and birth and death rates is linear. This was stated explicitly above and is put here as a reminder. We could have assumed a variety of relationships (logarithmic, exponential, hyperbolic, etc.)
2. The resource base of the population is constat, so that the carrying capacity is a constant. This is stated implicitly above, becasue b₀, d₀, v and z are all constants and so, logically, K is a constant.

It is possible to use the rules of calculus to integrate the growth rate equation to calculate the population size at a given time if the initial population size (N₀ is known). We won't do the math here, but will give the equation:

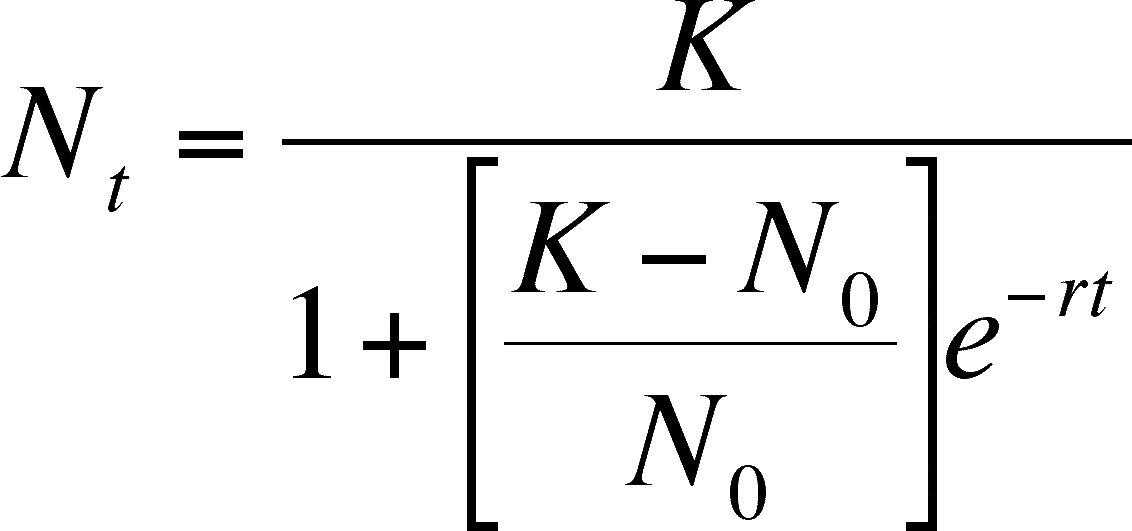
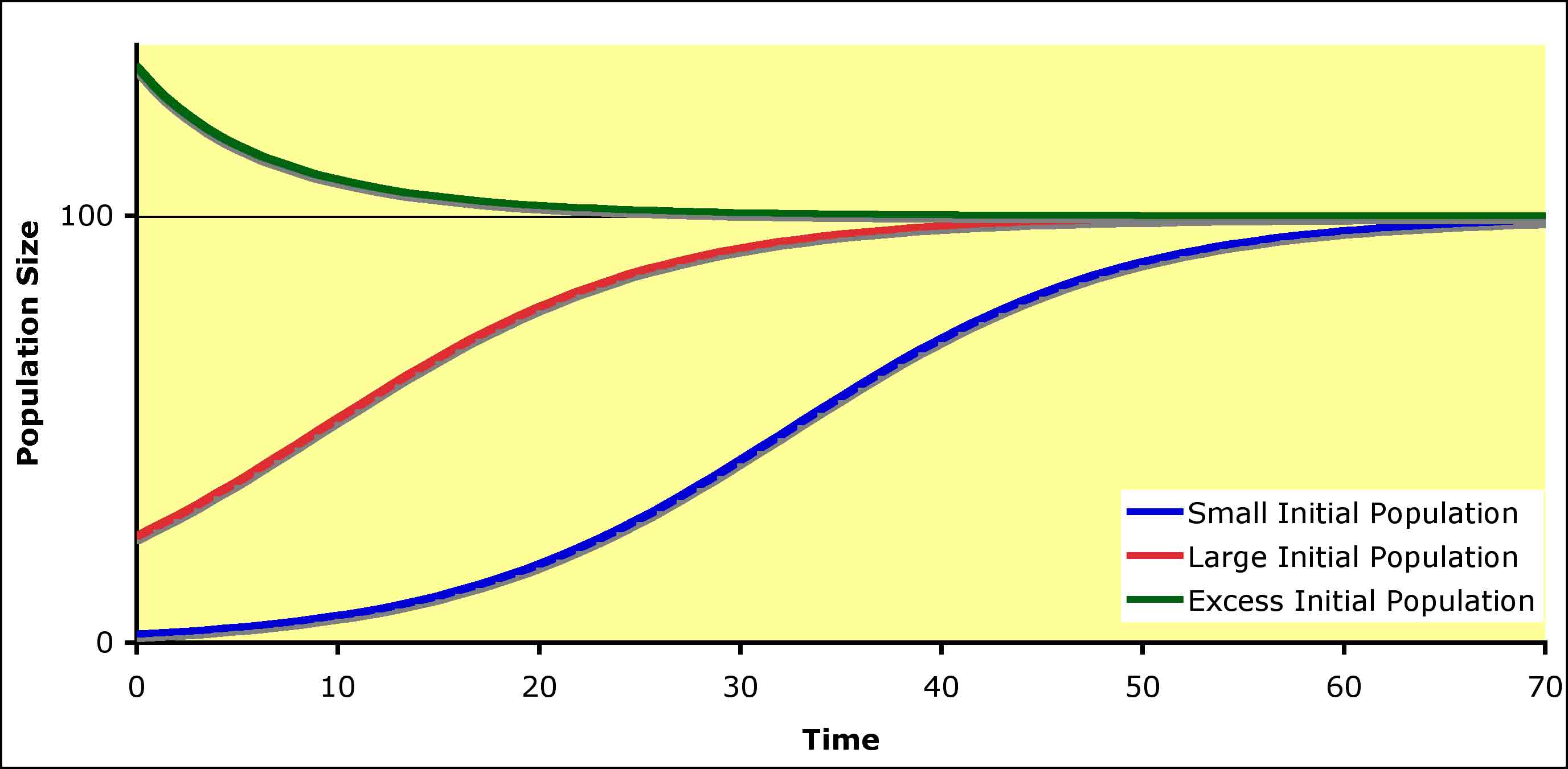
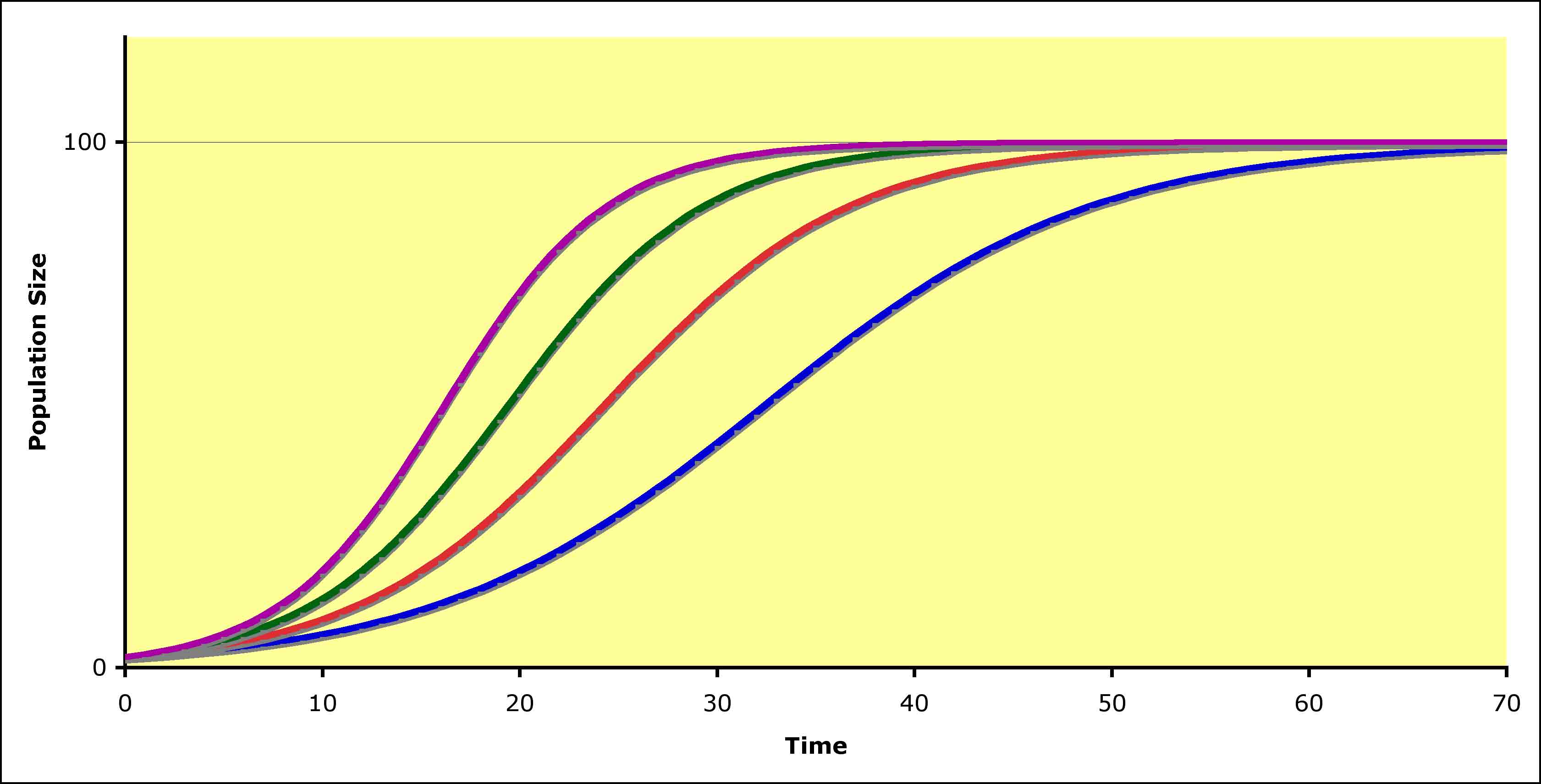
When you calculate growth rates with this equation and start with N near 0, you can plot a curve called a sigmoid curve (x-axis is time, y-axis is population size), which grows quickly at first, but the rate of increase drops off until it hits zero, at which there is no more increase in N. Due to the continuous nature of this equation, K is actually an asymptote, a limiting value that the equation never actually reaches. This is where one is reminded that the logistic is a model and will not behave exactly as a real population would, as a real population can grow by no less than one individual and this equation predicts growth (when close to K) of fractional individuals.

Let's look at the effect of changing some of the parameters in the prediction of future population size.  We will begin with the prediction for a population with a K of 100, an r of 0.16, and a minimum initial population size of 2.  The change in the population looks like this (blue line - Small Initial Population in the Key) - Remember K = 100:

• Note that the blue line is an "S" curve that never goes above 100 (technically it never gets to 100!), which is the carrying capacity, K
  • The curve has an inflection point, where the tangent lines stop getting steeper and start becoming flatter.
• What changes if you change the size of the initial population?
  • The larger initial population size (red - with an ititial population size of 25) line does not have the obvious "S" shape associated with the Logistic
    • Draw a line parallel to the X-axis the goes through 25, the large initial population size and you will see that the blue curve above that line looks just like the red curve.
  • The larger initial population size does not change the shape of the curve but it shifts it to the left.
  • If you start with a population size larger than K (the green line - Excess in the key - population size of 135), the shape is quite different.  The line approachs K but there is no hint of an S
• What is the effect of changing the intrinsic growth rate, r?

• The difference in the four lines is r (K = 100 for all and the initial population size is 2 for all four cases) is how quickly they approach the carrying capacity

Problems:

1. Do a dimensional analysis on the term (b₀ - d₀)/(v + z) to prove that the dimension of K is individuals.
2. Graph the last equation for the following parameters: r = 0.4, N₀ = 10, K = 100, t = 1 through 20 days). By choosing particular graphing options, you can produce a smooth sigmoid curve.
3. What is the predicted Nt (using the parameters above) when t is 1000 days? Have you exceeded the asymptote of 100 individuals?
4. Graph the last equation for the following parameters: r = 0.4, N₀ = 190, K = 100, t = 1 through 20 days).

Literature Cited

Lotka, A. J. 1925. Elements of Physical Biology. Williams and Wilkins, pubs., Baltimore.

Verhulst, P. F. 1839. Notice sur la loi que la population suit dans son accroissement. Correspondence in Mathematics and Physics 10:113-121.

Last Updated on March 2, 2007